人脸特征点置信度算法

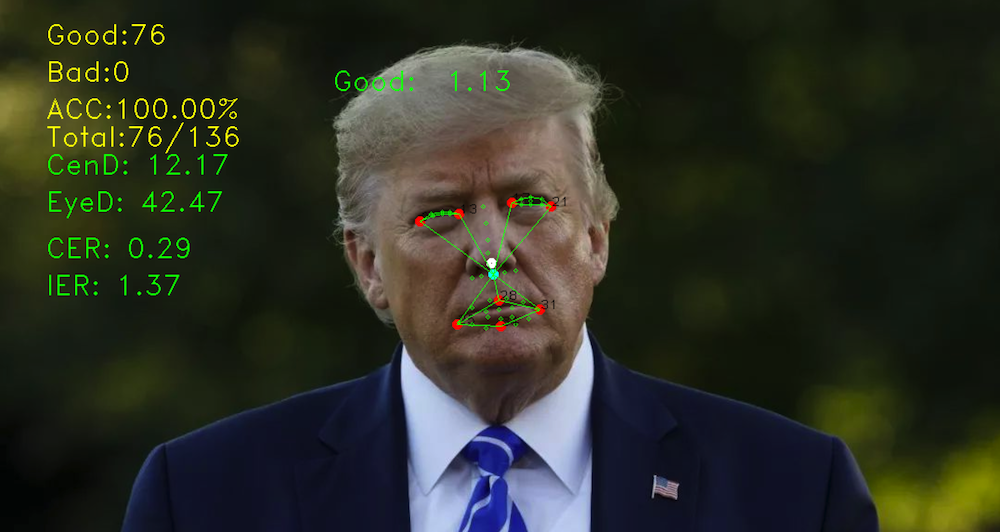
使用训练好的模型进行人脸特征点标记的时候，经常会生成一些特征点标记不准确、顺序错误或散乱的数据，每次标记完成后还要再经过人工进行筛选，特别耗时，少量数据还好，对于大数据集来说简直就是灾难。针对此种情况，根据人脸面部特征的规律现总结出一个算法用来计算特征点的置信度，给它起名叫FCC\(Facial Landmark Confidence Coefficient\)人脸置信度系数。该算法可以粗略的判断出模型标记的人脸特征点是否正确，使用人工标记的数据对算法进行测试，其有效识别率在95%左右。为了提高算法的可靠性又加入了两个辅助系数，CER和IER。在辅助系数的共同作用下有效识别率在97.65%以上。目前该算法还有待优化，有效识别率为97.65%也就意味着误判率为3左右%，每100张就有3张误判，每10000张误判数量就会高达300张。如果使用这些数据再进行其他网络的训练就会影响新模型的准确度。为了尽可能降低算法的误判率，我们可以对系数范围进行微调。例如 0.85 < FCC <= 1.9 识别率为97.65%，而 0.82 < FCC <= 2.3 时，可以将有效识别率提高至98.6%。这样做也有一个风险，强行扩大系数范围虽然能够少量提高有效识别率，但却使得有效识别的数据极有可能存在伪数据，所以在不同的场景下想要微调系数还需要斟酌。

在讲解算法之前先看一张图，如下图所示（非专业绘画，勉强一观吧）。图中的眼睛位置以我们为参考，其中 L 代表左眼，R 代表右眼， n 代表鼻子下方的人中，m 代表嘴巴，下标是每个点的序号。左右眼各8点，人中5点，嘴巴4点。

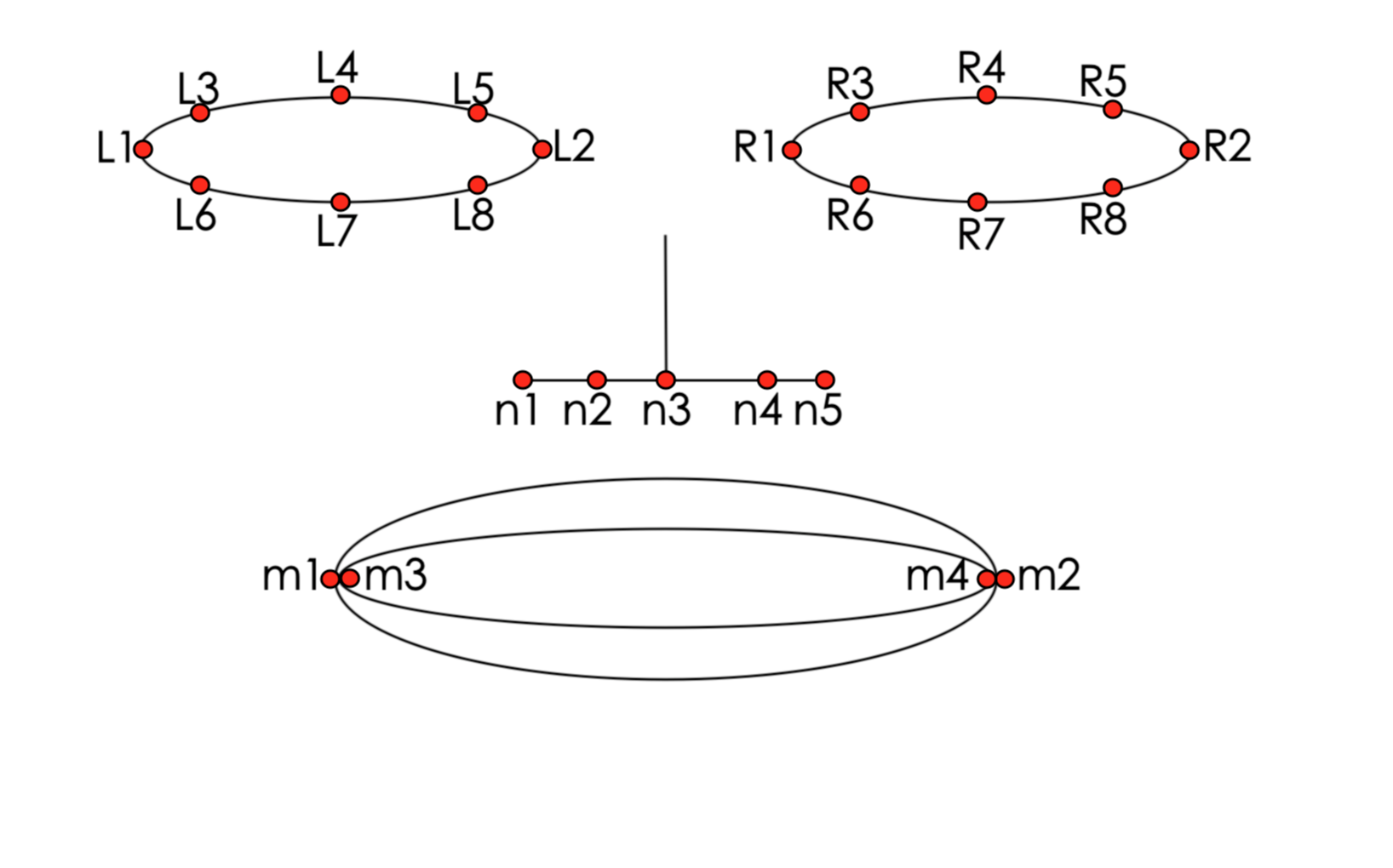
一、 FCC(Facial Landmark Confidence Coefficient)

经实践及大量数据的佐证，发现人脸五官（睁闭眼、左右上下摇头、张闭嘴角及）特征点存在着既定的系数联系，由此为出发点随机从公开数据集中抽取欧美与亚洲等部分地区的数据作为基础进行验证，通过实验与特定的处理方法最终得出一些规律系数，我们可暂时称它为人脸特征点置信度系数（FCC）。现将人脸特征点置信度系数的计算方法进行总结并抽象为数学公式，接下来我将对FCC的推导及计算过程进行简单的讲解。

1. 人中中点与眼睛的系数

\(E_1\) = \(\sqrt[2]{NC^2+[mean(L_i)i\in[1,2]]^2}\)

\(E_2\) = \(\sqrt[2]{NC^2+[mean(R_i)i\in[1,2]]^2}\)

\(E_3\) = \(\sqrt[2]{NC^2+[mean(L_i)i\in[1,8]]^2}\)

\(E_4\) = \(\sqrt[2]{NC^2+[mean(R_i)i\in[1,8]]^2}\)

• NC为人中5点的均值坐标，或者称为人中的中点坐标
• \(E_i\)是NC到左右眼的各均值点的距离

\(Eye Coefficient = \frac{1}{4}\displaystyle \sum^{4}_{i=1}E_i\)

Eye Coefficient表示人中中点与眼睛的系数，该系数主要表示为人中中点到左右眼各均值点的距离平均值，其中\(E_1\)E1是NC到\(L_1\)L1和\(L_2\)L2的均值点距离，同理\(E_3\)E3是NC到\(L_1\)L1-\(L_8\)L8, 8点均值的距离。

2. 人中中点与嘴角的系数

\(Mouth Coefficient = \frac{1}{4}\displaystyle \sum^{4}_{i=1} \sqrt[2]{NC^2+m^2_i}\)

• \(m_i\)m_i 嘴角的4点坐标
• Mouth Coefficient 是NC到嘴角4点的距离均值

3. 眼睛与嘴角系数的比

为了方便后续参与运算，此处我们可以使用一些缩写字母来表示该系数,将眼睛与嘴角的系数用EMR(Eye Mouth Ratio)来表示 \(EMR=\frac{Eye Coefficient}{Mouth Coefficient}=\frac{\frac{1}{4}\displaystyle \sum^{4}_{i=1}E_i}{\frac{1}{4}\displaystyle \sum^{4}_{i=1} \sqrt[2]{NC^2+m^2_i}}=\frac{\displaystyle \sum^{4}_{i=1}E_i}{\displaystyle \sum^{4}_{i=1} \sqrt[2]{NC^2+m^2_i}}\) EMR 可以用来表示以NC为比例点，人脸上半部分与下半部分的比例系数，该系数可以用来粗略定位人脸整体的关系，特征点是否存在大的偏差。

4. 左右眼关联系数

左右眼关联系数用来互相限定眼睛的大致位置，可以用EDR(Eye Distance Ratio)来表示 \(EDR=\sqrt[2]{\frac{L^2_1+R^2_1}{L^2_2+R^2_2}}\)

1. 左右眼眼宽系数

左右眼宽系数可用于检测眼宽是否异常，使用EWR(Eye Width Ratio)来表示

\(EWR = \frac{min(\sqrt[2]{L^2_1+L^2_2}, \sqrt[2]{R^2_1+R^2_2})}{max(\sqrt[2]{L^2_1+L^2_2}, \sqrt[2]{R^2_1+R^2_2})}\)

\(min(\sqrt[2]{L^2_1+L^2_2}, \sqrt[2]{R^2_1+R^2_2})\)

\(max(\sqrt[2]{L^2_1+L^2_2}, \sqrt[2]{R^2_1+R^2_2})\)

6. 面部置信度系数

\(FCC = \frac{1}{3}(EMR + EDR + EWR)=\frac{1}{3}(\frac{\displaystyle \sum^{4}_{i=1}E_i}{\displaystyle \sum^{4}_{i=1} \sqrt[2]{NC^2+m^2_i}} + \sqrt[2]{\frac{L^2_1+R^2_1}{L^2_2+R^2_2}} + \frac{min(\sqrt[2]{L^2_1+L^2_2}, \sqrt[2]{R^2_1+R^2_2})}{max(\sqrt[2]{L^2_1+L^2_2}, \sqrt[2]{R^2_1+R^2_2})})\) FCC 面部置信度系数， 0.85 < FCC <= 1.9

二、辅助系数CER

CER可以很方便的检测出面部四角区域的混乱程度，当值超出范围值时，眼睛与嘴角会出现较大的扭曲。 \(CER = \frac{2\sqrt[2]{NC^2 + [mean(L_i, R_i, M_j)i\in[1,2],j\in[1,4]]^2}}{\sqrt[2]{L^2_1+L^2_2} + \sqrt[2]{R^2_1+R^2_1}}\) CER(Face Center Eye Ratio)是用于恒量左眼、右眼和嘴角所连多边形混乱程度的系数

• 1.2 < CER <= 0

三、辅助系数IER

IER可以近一步规范眼睛区域的特征点，例如常见的大小眼、左右眼重叠、眼距过大或过小等情况 \(IER = \frac{2\sqrt[2]{L^2_2+R^2_1}}{\sqrt[2]{L^2_1 + L^2_2} + \sqrt[2]{R^2_1 + R^2_2}}\)

• IER(Inside Eye Ratio)
• 0.8 <= IER <= 3.5

四、实际检测效果